Конденсатор
Материал из МагВики::Справочник по автозвуку и электронике
Конденса́тор (от лат. condense — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Содержание |
История
В 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку».
Свойства конденсатора
Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
Обозначение конденсаторов на схемах
В России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.728-74[2] либо международному стандарту IEEE 315—1975:
| Обозначение по ГОСТ 2.728-74 | Описание |
|---|---|
| Конденсатор постоянной ёмкости | |
| Поляризованный конденсатор | |
| Подстроечный конденсатор переменной ёмкости |
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 106 пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 — 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.
Характеристики конденсаторов
Основные параметры
Ёмкость
Основной характеристикой конденсатора является его ёмкость', характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью 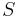 каждая, расположенных на расстоянии
каждая, расположенных на расстоянии 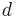 друг от друга, в системе СИ выражается формулой:
друг от друга, в системе СИ выражается формулой: 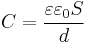 , где
, где 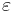 — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единица),
— относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единица), 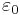 — электрическая постоянная, численно равная 8,854187817.10 - 12 (эта формула справедлива, лишь когда
— электрическая постоянная, численно равная 8,854187817.10 - 12 (эта формула справедлива, лишь когда 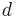 много меньше линейных размеров пластин).
много меньше линейных размеров пластин).
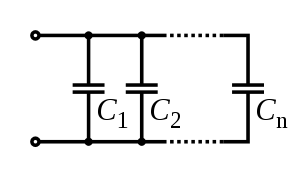
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
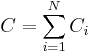 или
или
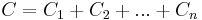
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счет разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.
Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
Удельная ёмкость
Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Плотность энергии
Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита. Например, у конденсатора EPCOS B4345 емкостью 12000 мкФ x 450 В и массой 1.9кг плотность энергии составляет 639Дж/кг или 845Дж/л. Особенно важен этот параметр при использовании конденсатора в качестве накопителя энергии, с последующим мгновенным её высвобождением, например, в пушке Гаусса
Номинальное напряжение
Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.
Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается, что связано с увеличением тепловой скорости движения носителей заряда и, соответственно, снижению требований для образования электрического пробоя.
Полярность
Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.
Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе (часто можно заметить её в форме буквы X, K или Т на торце). При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков.

Паразитные параметры
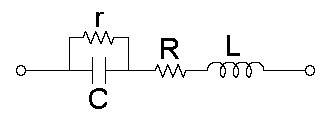
Реальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом:
|
Электрическое сопротивление изоляции конденсатора — r
Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением r = U / Iут , где U — напряжение, приложенное к конденсатору, Iут — ток утечки.
Эквивалентное последовательное сопротивление — R
Эквивалентное последовательное сопротивление (ЭПС, англ. ESR) обусловлено главным образом электрическим сопротивлением материала обкладок и выводов конденсатора и контакта(-ов) между ними, а также потерями в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор.
В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства
Эквивалентная последовательная индуктивность — L
Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. На низких частотах (до единиц килогерц) обычно не учитывается в силу своей незначительности.
Саморазряд
С течением времени конденсатор теряет энергию за счёт саморазряда.
Тангенс угла потерь
Тангенс угла потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости.
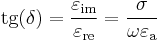
Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол 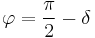 , где
, где 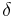 — угол диэлектрических потерь. При отсутствии потерь
— угол диэлектрических потерь. При отсутствии потерь 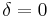 . Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная
. Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная 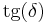 , называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.
, называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.
Температурный коэффициент ёмкости (ТКЕ)
ТКЕ — относительное изменение емкости при изменении температуры окружающей среды на один градус Цельсия (Кельвина). Таким образом, значение ёмкости от температуры представляется линейной формулой:
-
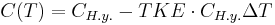 ,
,
где ΔT — увеличение температуры в °C или °К относительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Конденсаторы, имеющие нелинейную зависимость емкости от температуры, и конденсаторы с большими уходами емкости от воздействия температуры окружающей среды в обозначении имеют указание на относительное изменение емкости в рабочем диапазоне температур.
Диэлектрическое поглощение
Если заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение медленно повышается. Это явление получило название диэлектрическое поглощение или адсорбция электрического заряда. Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора. Подобный эффект можно наблюдать и на большинстве электролитических конденсаторов, но в них он является следствием химических реакций между электролитом и обкладками. Наименьшим диэлектрическим поглощением обладают конденсаторы с органическими диэлектриками: тефлон (фторопласт), полистирол, полиэтилентерефталат, поликарбонат.
Классификация конденсаторов
Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др. Кроме того, конденсаторы различаются по возможности изменения своей ёмкости В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и другие конденсаторы. Также различают конденсаторы по форме обкладок: плоские, цилиндрические, сферические и другие.
| Название | Ёмкость | Электрическое поле | Схема |
|---|---|---|---|
| Плоский конденсатор | 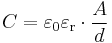 | 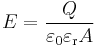 | 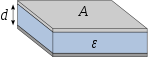 |
| Цилиндрический конденсатор | 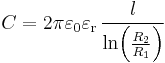 | 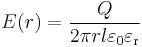 | 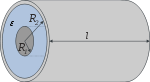 |
| Сферический конденсатор | 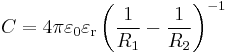 | 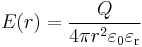 | 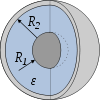 |
| Сфера | 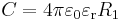 |
Применение конденсаторов
Конденсаторы находят применение практически во всех областях электротехники.
- Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п..
- При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, электромагнитных ускорителях, импульсных лазерах с оптической накачкой, генераторах Маркса, (ГИН; ГИТ), генераторах Кокрофта-Уолтона и т. п.
- Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
- В промышленной электротехнике конденсаторы используются для компенсации реактивной мощности и в фильтрах высших гармоник.
- Конденсаторы способны накапливать большой заряд и создавать большую напряженность на обкладках, которая используется для различных целей, например, для ускорения заряженных частиц или для создания кратковременных мощных электрических разрядов (см. генератор Ван де Граафа).
- Измерительный преобразователь (ИП) малых перемещений: малое изменение расстояния между обкладками очень заметно сказывается на ёмкости конденсатора.
- ИП влажности воздуха, древесины (изменение состава диэлектрика приводит к изменению емкости).
- В схемах РЗиА конденсаторы используются для реализации логики работы некоторых защит. В частности, в схеме работы АПВ использование конденсатора позволяет обеспечить требуемую кратность срабатывания защиты.
- Измерителя уровня жидкости. Непроводящая жидкость, заполняет пространство между обкладками конденсатора, и ёмкость конденсатора меняется в зависимости от уровня
- В качестве буферной емкости в цепи питания усилителя саббуферного канала в АЗ. Емкость его исчисляется фарадами и носит он другое толкование - ионистор.


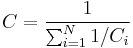 или
или
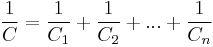
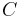 — собственная ёмкость конденсатора;
— собственная ёмкость конденсатора;
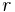 — сопротивление изоляции конденсатора;
— сопротивление изоляции конденсатора;
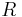 — эквивалентное последовательное сопротивление;
— эквивалентное последовательное сопротивление;
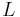 — эквивалентная последовательная индуктивность.
— эквивалентная последовательная индуктивность.
